Integrator

The secret

In our implementation, the PC doesn't sends any position or speed information to the FPGA. Instead, it sends acceleration and time information. The FPGA uses integrators to convert them into speed and position (and drives the Step/Dir signals accordingly).

So our motion controller works as an acceleration integrator. That's easy to implement because in an FPGA, an integrator is simply an accumulator. The following "C" code illustrates what the FPGA performs at each clock cycle:

  // Acceleration is known (provided by the PC)
  Speed += Acceleration;
  Position += Speed;

Acceleration integrator example

Let's illustrate that by an example: we want to move an axis by +50.

We could do the following:

1. Accelerate by +1 for 5 clock cycles.
2. Accelerate by 0 for 5 clock cycles.
3. Accelerate by -1 for 5 clock cycles.

After 15 clock cycles, our integrator has reached the position +50.

Cycle	Acceleration	Speed	Position
0	0	0	0
1	+1	+1	+1
2	+1	+2	+3
3	+1	+3	+6
4	+1	+4	+10
5	+1	+5	+15
6	0	+5	+20
7	0	+5	+25
8	0	+5	+30
9	0	+5	+35
10	0	+5	+40
11	-1	+4	+44
12	-1	+3	+47
13	-1	+2	+49
14	-1	+1	+50
15	-1	0	+50

Easy, right?

Fixed point precision arithmetic

Now there is a problem: the FPGA clock runs much faster than the steppers can accept steps. So the calculations must be done on fractional numbers. For example, we could decide that the position 50 above represents actually 0.000050mm in the hardware.

After careful consideration, we decided to use 64 bits fixed point precision arithmetic.
In more details:

• Acceleration uses 16 bits.
• Speed uses 40 bits.
• Position uses 64 bits. The stepper position is in the 20 more significant bits (bits 44 to 63). Every time the step bit (bit 44) changes, a step pulse is sent to a stepper motor.

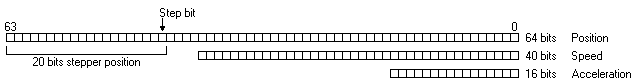
Of course, with a 3-axis system, we have 3 of each (3 positions, 3 speeds and 3 acceleration registers). The PC provides groups of 3 accelerations numbers (16 bits each), plus a duration, and the FPGA calculates the speeds and positions automatically using integrators.

>>> NEXT: FPGA motion controller >>>

---

This page was last updated on October 08 2007.