 |
|
To generate arbitrary signals, DDSs rely on two main tricks.
The first DDS trick is a LUT (lookup table). The LUT is a table that holds the shape of the signal we want to generate.
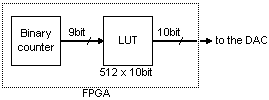
In an FPGA, the LUT is implemented as blockrams. In the picture above, we used a 512x10 bits LUT, which usually fits into one or two FPGA blockrams.
The most commonly generated signal shape is a sine wave. It is particular as it has two symmetries that can be easily exploited to make the LUT appear bigger.
In a sine wave, the first symmetry is sin(α)=sin(π-α).
Assuming our "my_DDS_LUT" blockram is instantiated like that
wire [9:0] LUT_output;
blockram512x10bits_2clklatency
my_DDS_LUT(
.rdclock(clk),
.rdaddress(cnt[8:0]),
.q(LUT_output)
);
we simply have to write this below to exploit the first symmetry.
wire [9:0] LUT_output;
blockram512x10bits_2clklatency
my_DDS_LUT(
.rdclock(clk),
.rdaddress(cnt[9] ? ~cnt[8:0] : cnt[8:0]), // reverse the direction of reading the LUT after a half-period
.q(LUT_output)
);
So now we store only half of the wave in the blockram, but its content is used twice for each period of the output signal. In a sense, the LUT appears as a 1024x10bits. Using the second symmetry, we get a 2048x10bits.
Note that we use a blockram "blockram512x10bits_2clklatency" that provides data with two clocks latency (one clock latency blockrams are usually slow). How this is done is FPGA vendor dependent (Altera would use LPMs while Xilinx would use primitives).
Let's rewrite the LUT as a separate module that exploits the two sine symmetries.
// sine lookup value module using two symmetries
// appears like a 2048x10bits LUT even if it uses a 512x10bits internally
// 3 clock latency
module sine_lookup(clk, addr, value);
input clk;
input [10:0] addr;
output [16:0] value;
wire [15:0] LUT_output;
blockram512x16bits_2clklatency
my_DDS_sine_LUT( // the LUT must contain only one quarter of the sine wave
.rdclock(clk),
.rdaddress(addr[9] ? ~addr[8:0] : addr[8:0]), // first symmetry
.q(LUT_output)
);
// for the second symmetry, we need to use addr[10]
// but since we use a blockram that has 2 clock latencies on reads
// we need a two-clock delayed version of addr[10] here
reg addr10_delay1; always @(posedge clk) addr10_delay1 <= addr[10];
reg addr10_delay2; always @(posedge clk) addr10_delay2 <= addr10_delay1;
// now we can apply the second symmetry (and add a third latency to the module output for best performance)
reg [16:0] value; always @(posedge clk) value <= addr10_delay2 ? {1'b0,-LUT_output} : {1'b1,LUT_output};
endmodule
Note that the sine_lookup module has a total of 3 clock latencies (two from the blockram, and one from the registered output at the end).
Having clock latencies has the benefit of pipelining the operation and getting the maximum possible performance out of the FPGA.
Don't forget that this needs to run at at least 100MHz.
Also we increased the output width of our blockram from 10 bits to 16 bits (the 6 extra bits are lost if unused in our particular FPGA blockram, so we might as well implement them). We'll put the extra bits in good use in part 4.
To effectively use our newly made "sine_lookup module", we can simply write
reg [10:0] cnt;
always @(posedge clk) cnt <= cnt + 11'h1;
wire [16:0] sine_lookup_output;
sine_lookup my_sine(.clk(clk), .addr(cnt), .value(sine_lookup_output));
wire [9:0] DAC_data = sine_lookup_output[16:7]; // for now, we drop the LSBs to feed our DAC
// (since it takes only 10 bits)
and we get a nice sine wave from the DAC.